Nächste Seite: Der Buchberger-Algorithmus (II) Aufwärts: Gröbnerbasen Vorherige Seite: Der Buchberger-Algorithmus
(Fortsetzung, F = {f1, f2} wie oben.)
G0 = F, dann
S(f1, f2)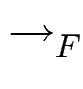 x2 - y2 = f3, also
G1 = {f1, f2, f3}.
Neue Paare
S(f1, f3) = f1 - yf3 = y3 - y2 = : f4 ist Normalform,
S(f2, f3) = xf2 - y2f3 = - xy2 + y4
x2 - y2 = f3, also
G1 = {f1, f2, f3}.
Neue Paare
S(f1, f3) = f1 - yf3 = y3 - y2 = : f4 ist Normalform,
S(f2, f3) = xf2 - y2f3 = - xy2 + y4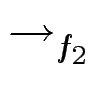 y4 - y2
y4 - y2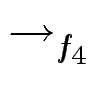 y3 - y2
y3 - y2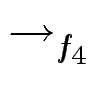 0.
0.
mit Mupad:
groebner::gbasis([x^2*y-x^2,x*y^2-y^2],DegreeOrder)