Der Buchberger-Algorithmus

Eingabe: endliche Menge F von Polynomen und Ordnung > auf Monomen.
Ausgabe: eine Gröbnerbasis G für Ideal(F).

1. Beginne mit G : = F.

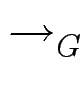2. wähle f₁, f₂ $\in$ G, bestimme eine $\to_{G}^{}$-Normalform s von S(f₁, f₂).

3. falls s $\neq$ 0, füge s zu G hinzu und gehe zu 2.

4. falls man in (2.) nicht so wählen konnte, daß in (3.) s $\neq$ 0, dann Ausgabe G.

Satz: Dieser Algorithmus hält nach endliche vielen Schritten und gibt eine Gröbnerbasis G für F aus.

Den Test in (4.) muß man geeignet implementieren (man wird nicht immer alle Paare vergleichen)