S-Polynome

Man erhält eine Gröberbasis für eine gegebene Menge F durch Vervollständigung (Hinzufügen von Polynomen s $\in$ Ideal(F))

Für alle Paare f₁, f₂ $\in$ F: bestimme m = lcm(H(f₁), H(f₂)) (kleinstes gemeinsames Vielfaches der Köpfe), dann S(f₁, f₂) : = f₁ ^. m/H(f₁) - f₂ ^. m/H(f₂). Es gilt: S(f₁, f₂) $\in$ Ideal(F).

Beispiel ( F = {f₁, f₂} wie oben.) S(f₁, f₂) = f₁y - f₂x = x²y - xy²

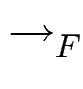Satz: Wenn für alle f₁, f₂ $\in$ F : S(f₁, f₂)$\to_{F}^{}$ 0, dann ist F eine Gröbnerbasis.

Beispiel: x²y - xy²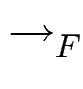$\to_{F}^{}$x² - y² 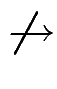$\not\to$_F0.