Nächste Seite: S-Polynome Aufwärts: Gröbnerbasen Vorherige Seite: Reduktion von Polynomen
die eben definierte Relation
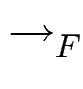 ist nicht notwendig konfluent.
ist nicht notwendig konfluent.
Beispiel (8.2.10 aus Baader/Nipkow) F = {f1, f2} mit f1 = x2y - x2, f2 = xy2 - y2. Ordnung > auf Monomen: erst nach Exponentensumme, dann lexikografisch.
x2y2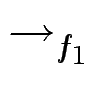 x2y2 - y . f1 = x2y
x2y2 - y . f1 = x2y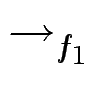 x2y - 1 . f1 = x2
und
x2y2
x2y - 1 . f1 = x2
und
x2y2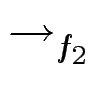 ?
?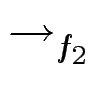 y2.
Beides sind Normalformen, also
y2.
Beides sind Normalformen, also 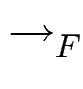 nicht konfluent.
nicht konfluent.
Definition:
eine endliche Menge G von Polynomen heißt Gröbnerbasis
für ein Polynomideal I, falls
Ideal(G) = I und 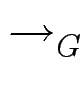 konfluent.
konfluent.
Nicht-Beispiel (Fortsetzung) F ist keine Gröbnerbasis.