Reduktion von Polynomen

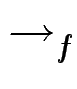p$\to_{f}^{}$q, falls p ein Monom a ^. m enthält und ein m' exist. mit m = H(f )m' und q = p - am'f.

F eine endliche Menge von Polynomen, dann definiere 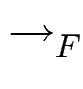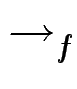$\to_{F}^{}$ = $\bigcup${$\to_{f}^{}$ | f $\in$ F}.

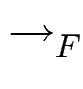Satz: $\to_{F}^{}$ terminiert immer.

Beweis-Idee: wenn g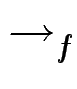$\to_{f}^{}$g', dann wird in g das Monom H(f ) gelöscht und durch eventuell mehrere, aber jedenfalls kleinere ersetzt. Weil > auf Monomen nach Voraussetzung terminiert, terminiert auch die dadurch erzeugte Ordnung auf Polynomen, die man so definiert: p $\gg$ q falls: Monome jeweils bzgl. > absteigend sortieren und dann beide Folgen lexikografisch vergleichen. Beachte: da werden immer nur die Monome (ohne Koeffizienten) verglichen.