Beispiel (Minimal-)Polynom

y = $\sqrt{{2}}$ + $\sqrt[3]{{3}}$ bestimme alle Koeffizienten

M = $$\begin{array}{c\vert cccccc} & 1 & \sqrt[3]{3} & \sqrt{2} & \... ...^5 & 60& 20& 4 & 15& 3 & 20 \ \hline y^6 & 17& 90&120& 24& 60& 18 \end{array}$$

nenne die Zeilenvektoren x₀,..., x₆, löse lineare Gleichung

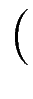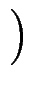$$\left(\vphantom{ x_0^T \ldots x_5^T }\right.$$x₀^T...x₅^T$$\left.\vphantom{ x_0^T \ldots x_5^T }\right)$$ ^. c^T = x₆^T

ergibt Koeffizientenvektor c = (- 1, 36, - 12, 6, 6, 0), d. h. -1 + 36y - 12y² +6y³ +6y⁴ = y⁶. Ein Polynom mit Nullstelle y ist deswegen

y⁶ -6y⁴ -6y³ +12y² - 36y + 1

.