Nächste Seite: Gröbnerbasen Aufwärts: Algebraische Zahlen Vorherige Seite: Beispiel (Minimal-)Polynom
gegeben eine (hochgenaue) Näherung x einer algebraischen Zahl, gesucht das dazugehörige Polynom.
Bestimme eine kurzen Vektor in dem Gitter, das durch diese Spaltenvektoren aufgespannt wird:
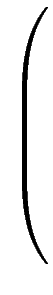
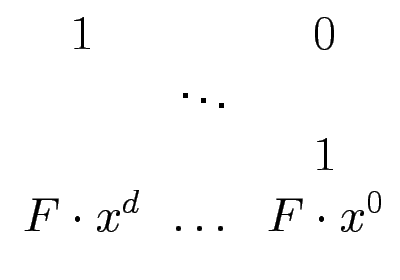
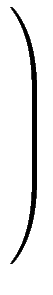
Matrix berechnen durch diese Mupad-Funktion
M := (x, d, f) -> [[(if s = z then
1
else
if z = d + 1 then
round(f*x^((d + 1) - s))
else
0
end_if
end_if) $ s = 0..d] $ z = 0..d + 1]
DIGITS := 50
x:=2^(1/2)+3^(1/3)
kurzen Gittervektor finden durch LLL-Algorithmus (Lenstra,Lenstra,Lovasz), findet nicht den kürzesten, hat dafür aber vernünftige Laufzeit.
lllint (M(x,6,10^40) -- verschiedene Dimensionen probierenliefert Kandidaten für Koeffizienten eines Polynoms mit Nullstelle x.
Andere Anwendung (Übung): finde nahe beieinanderliegende (Primzahl-)Produkte Matrix wie oben, untere Zeile besteht aus F log(2), F log(3), F log(5), F log(7). Für F = 106 findet man die Koeffizienten [4, - 2, 11, - 2, - 6], das entspricht 24511 = 781250000, 32*72*116 = 781258401. vgl. abc-Vermutung und Tabelle http://www.mathematik.uni-jena.de/~aros/abc.html