Gebrochen rationale Funktionen

• haben allgemeine Form f (x) = $${\frac{{ax + b}}{{cx +d}}}$$
• Notation als Matrix [f] = $\left(\vphantom{\begin{array}{cc}a &b \ c& d \end{array}}\right.$$\begin{array}{cc}a &b \ c& d \end{array}$$\left.\vphantom{\begin{array}{cc}a &b \ c& d \end{array}}\right)$
• ist nützlich, denn es gilt [fog] = [f] ^. [g]

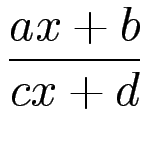
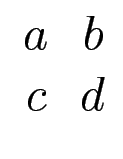
betrachte Kettenbruch k = [a₀;a₁,..., a_n]
als Funktion x $\mapsto$ [a₀;a₁,..., a_n, x]

[k] = $\left(\vphantom{\begin{array}{cc}1 & a_0 \ 0 & 1 \end{array}}\right.$$\begin{array}{cc}1 & a_0 \ 0 & 1 \end{array}$$\left.\vphantom{\begin{array}{cc}1 & a_0 \ 0 & 1 \end{array}}\right)$$\left(\vphantom{\begin{array}{cc}0 & 1 \ 1 & 0 \end{array}}\right.$$\begin{array}{cc}0 & 1 \ 1 & 0 \end{array}$$\left.\vphantom{\begin{array}{cc}0 & 1 \ 1 & 0 \end{array}}\right)$$\left(\vphantom{\begin{array}{cc}1 & a_1 \ 0 & 1 \end{array}}\right.$$\begin{array}{cc}1 & a_1 \ 0 & 1 \end{array}$$\left.\vphantom{\begin{array}{cc}1 & a_1 \ 0 & 1 \end{array}}\right)$$\left(\vphantom{\begin{array}{cc}0 & 1 \ 1 & 0 \end{array}}\right.$$\begin{array}{cc}0 & 1 \ 1 & 0 \end{array}$$\left.\vphantom{\begin{array}{cc}0 & 1 \ 1 & 0 \end{array}}\right)$...$\left(\vphantom{\begin{array}{cc}1 & a_n \ 0 & 1 \end{array}}\right.$$\begin{array}{cc}1 & a_n \ 0 & 1 \end{array}$$\left.\vphantom{\begin{array}{cc}1 & a_n \ 0 & 1 \end{array}}\right)$$\left(\vphantom{\begin{array}{cc}0 & 1 \ 1 & 0 \end{array}}\right.$$\begin{array}{cc}0 & 1 \ 1 & 0 \end{array}$$\left.\vphantom{\begin{array}{cc}0 & 1 \ 1 & 0 \end{array}}\right)$

= $\left(\vphantom{\begin{array}{cc}a_0 & 1 \ 1 & 0 \end{array}}\right.$$\begin{array}{cc}a_0 & 1 \ 1 & 0 \end{array}$$\left.\vphantom{\begin{array}{cc}a_0 & 1 \ 1 & 0 \end{array}}\right)$$\left(\vphantom{\begin{array}{cc}a_1 & 1 \ 1 & 0 \end{array}}\right.$$\begin{array}{cc}a_1 & 1 \ 1 & 0 \end{array}$$\left.\vphantom{\begin{array}{cc}a_1 & 1 \ 1 & 0 \end{array}}\right)$...$\left(\vphantom{\begin{array}{cc}a_n & 1 \ 1 & 0 \end{array}}\right.$$\begin{array}{cc}a_n & 1 \ 1 & 0 \end{array}$$\left.\vphantom{\begin{array}{cc}a_n & 1 \ 1 & 0 \end{array}}\right)$

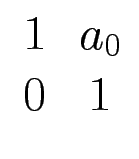
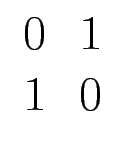
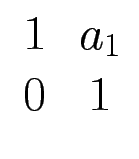
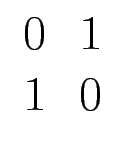
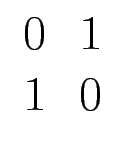
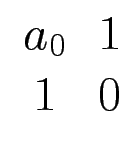
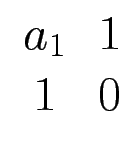
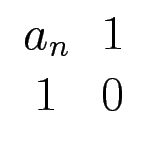
...das kann man auch mit mupad ausrechnen:

f := (a -> matrix([[a,1],[1,0]]))
f(1) * f(2) * f(2) * f(2)

Wert eines periodischen Kettenbruchs ergibt sich als Fixpunkt der gebr. rationalen Funktion, die der Periode entspricht.

Periode 2: [f (2)](x) = x

linalg::eigenvalues (f(2))