Nächste Seite: Kritische Paare Aufwärts: Terme, Ersetzungs-Systeme Vorherige Seite: Konfluenz
Eine zweistellige Relation ![]() heißt lokal konfluent, wenn
heißt lokal konfluent, wenn
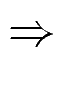
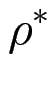 (y1, z)
(y1, z) 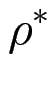 (y2, z)
(y2, z)
Beachte: es gibt Relationen ![]() ,
die lokal konfluent sind, aber nicht konfluent.
,
die lokal konfluent sind, aber nicht konfluent.
Satz: wenn ![]() terminiert und lokal konfluent ist,
dann ist
terminiert und lokal konfluent ist,
dann ist ![]() konfluent.
konfluent.