Nächste Seite: Lokale Konfluenz Aufwärts: Terme, Ersetzungs-Systeme Vorherige Seite: Term-Ersetzung und Computeralgebra
Eine zweistellige Relation ![]() heißt konfluent, wenn
heißt konfluent, wenn
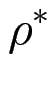 (x, y1)
(x, y1) 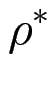 (x, y2)
(x, y2) 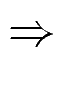
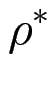 (y1, z)
(y1, z) 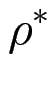 (y2, z)
(y2, z)
Satz: wenn ![]() auf M konfluent ist,
dann besitzt jedes x
auf M konfluent ist,
dann besitzt jedes x ![]() M
höchstens eine
M
höchstens eine ![]() -Normalform.
-Normalform.
Beachte: es wird nicht behauptet, daß x überhaupt eine Normalform besitzt.
Falls ![]() jedoch terminiert,
dann läßt sich Konfluenz charakterisieren und entscheiden
durch einen Hilfsbegriff (lokale Konfluenz, später)
jedoch terminiert,
dann läßt sich Konfluenz charakterisieren und entscheiden
durch einen Hilfsbegriff (lokale Konfluenz, später)