Multiplikation Boolescher Matrizen

(im Booleschen Halbring: plus = or, mal = und)

Für A ^. B, beide quadratisch n×n,

zerlege A in vertikale Streifen, B in horizontale, gleicher Breite l, dann AB = 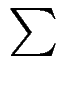$\sum$A_iB_i.

Jeder Streifen A_i besteht aus Zeilen A_{i, j} (der Breite l)

Jedes Produkt A_{i, j} ^. B_i ist eine Linearkombination der Zeilen von B_i.

Trick: alle 2^l Kombinationen vorher berechnen und speichern! benötigt 2^ln Platz (und Zeit)

A ^. B benötigt dann noch (n/l )n² Zeit. Geeignetes l?

Der ,,Vier-Russen-Algorithmus``

http://www14.in.tum.de/skripten/ead_ws9899_html/node94.html