Matrix-Multiplikation nach Strassen

$$\left(\vphantom{\begin{array}{cc}a&b\ c&d \end{array}}\right.$$$$\begin{array}{cc}a&b\ c&d \end{array}$$$$\left.\vphantom{\begin{array}{cc}a&b\ c&d \end{array}}\right)$$ ^. $$\left(\vphantom{\begin{array}{cc}e&f\ g&h \end{array}}\right.$$$$\begin{array}{cc}e&f\ g&h \end{array}$$$$\left.\vphantom{\begin{array}{cc}e&f\ g&h \end{array}}\right)$$ = $$\left(\vphantom{\begin{array}{cc}ae+bg&af+bh\ ce+dg&cf+dh \end{array}}\right.$$$$\begin{array}{cc}ae+bg&af+bh\ ce+dg&cf+dh \end{array}$$$$\left.\vphantom{\begin{array}{cc}ae+bg&af+bh\ ce+dg&cf+dh \end{array}}\right)$$

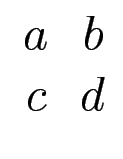
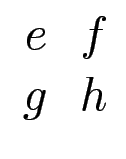
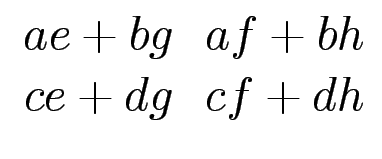
8 Mult, 4 Add.

Es genügen 7 Multiplikationen (welche?) und mehrere Additionen/Subtraktionen (welche?)

Dann T(n) = 7*T(n/2) + c ^. n

http://mathworld.wolfram.com/StrassenFormulas.html