Nächste Seite: On Numbers And Games Aufwärts: Zahlen, Vektoren, Gitter Vorherige Seite: Anwendung: ABC-Tripel
(z.B. log(1 + d ),
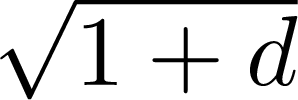 )
und (z.B.)
n = 3, d = 0.1
)
und (z.B.)
n = 3, d = 0.1
zeichnen Sie (zwei Kurven in ein Bild) (maxima: plot2d)
Bsp: log(1 + x) - (x - x2/2)
Welche Werte/Punkte in der Zeichnung sind zu vergleichen?
es gilt 2n+2 | 32n - 1, also c > rad(abc)⋅2n+1/3
vgl. Marc Saul https://cims.nyu.edu/cmt/assets/pdfs/HS_Problems/ABC_Conjecture.pdf
ABC@Home?