Nächste Seite: Motivation (III): Geometrische Örter Aufwärts: Polynome Vorherige Seite: Motivation (I): Polynom-Interpretationen
Bsp: gesucht ist Minimalpolynom für
y = 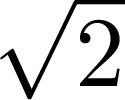 +
+ ![$\sqrt[3]{{3}}$](img5.png)
| 1 | ![$\displaystyle \sqrt[3]{{3}}$](img78.png) |
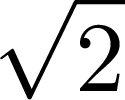 |
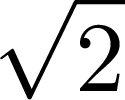 ![$\displaystyle \sqrt[3]{{3}}$](img78.png) |
![$\displaystyle \sqrt[3]{{3^2}}$](img80.png) |
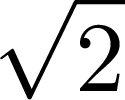 ![$\displaystyle \sqrt[3]{{3^2}}$](img80.png) |
|
| y0 | 1 | 0 | 0 | 0 | 0 | 0 |
| y1 | 0 | 1 | 1 | 0 | 0 | 0 |
| y2 | 2 | 0 | 0 | 2 | 1 | 0 |
| y3 | 3 | 6 | 2 | 0 | 0 | 3 |
| y4 | 4 | 3 | 12 | 8 | 12 | 0 |
| y5 | 60 | 20 | 4 | 15 | 3 | 20 |
| y6 | 17 | 90 | 120 | 24 | 60 | 18 |