Nächste Seite: Logik und Unentscheidbarkeit (II) Aufwärts: Uninterpretierte Funktionen (UF) Vorherige Seite: Gleichheit von Termen
Def: das Gültigkeitsproblem der Prädikatenlogik:
Beispiel: ![]() : zwei einstellige Funktionsymbole f, g,
: zwei einstellige Funktionsymbole f, g,
ein nullstelliges Funktionssymbol a,
ein zweistelliges Prädikatsymbol R.
  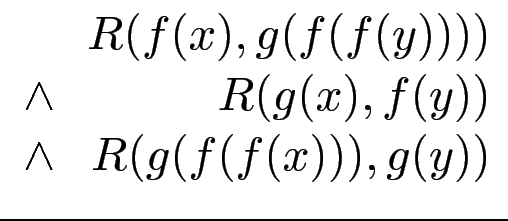  |
|||
| R(a, a) |