Vortragsankündigung, Bereichsseminar Theoretische Informatik,
Dienstag, den 23. (und 30. April) 2002, 13:15 - 14:45, Hauptgebäude Raum 3-68
Dr. J. Waldmann,
Institut für Informatik, Universität Leipzig
Term-Ersetzungs-Spiele
Zu einem gegebenen, terminierenden, Term- (oder Wort-)Ersetzungs-System R
und Startterm t spielen zwei Spieler A, B das folgende Spiel:
- ein Spielzug ist die Auswahl einer Regel aus R und
einer Position aus t, und die Anwendung dieser Regel an dieser Position.
- verloren hat, wer nicht mehr ziehen kann (weil der Term in Normalform ist).
Beispiel: Hier ist der komplette Spielgraph für das Spiel mit Regeln
{ 01 -> 10, 1 -> 2 } und das Startwort 011. Verlustpositionen sind umkreist.
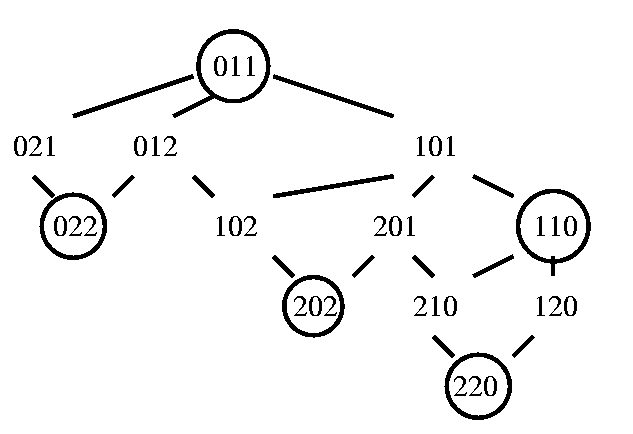
Aufgabe: zeige, daß für dieses Spiel
alle Positionen (01010101)^* verloren sind.
Nach Definition sind solche Spiele immer neutral (impartial,
beide Spieler haben gleiche Optionen)
und normal (wer als letzter zieht, gewinnt).
Damit kann man die Sprague-Grundy-Theorie zu ihrer Beschreibung heranziehen.
Eine seit langen Jahren offene Frage dieser Theorie
ist die nach der erschöpfenden Beschreibung gewisser
Take-und-Break-Spiele. Ich schlage vor, diese Frage
vom Standpunkt der Term-Ersetzung zu betrachten und Methoden anzuwenden,
die reguläre Baumsprachen benutzen.
Das führt andererseits zu einer Weiterentwicklung dieser Methoden selbst,
worauf ich im zweiten Vortrag genauer eingehen werde.
Literatur/Links:
Gäste sind herzlich eingeladen, insbesondere Studenten,
die an einer weiteren Beschäftigung mit diesem Thema
(von der Praktikums- bis hin zur Diplomarbeit) interessiert sind.
http://www.informatik.uni-leipzig.de/~joe/
mailto:joe@informatik.uni-leipzig.de

