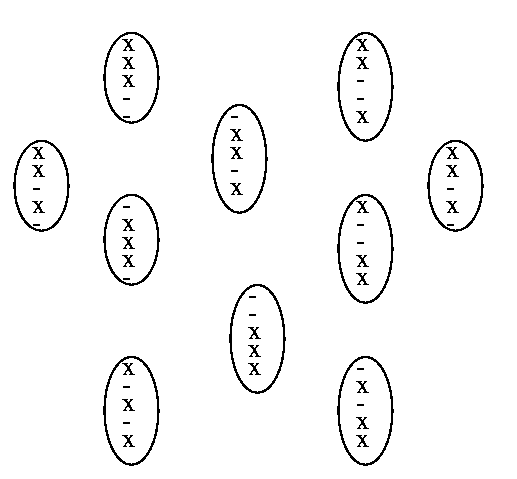
Beispiele
Da stellt sich sofort die Frage: wie lang können einfache Muster sein? Wir müssen die Ballzahl b und die maximale Höhe h begrenzen.
Dann gibt es (h über b) Zustände. Diese bilden einen gerichteten Graphen. Beispiel: b = 3, h = 5. Das sind (5 über 3) = (5 * 4 * 3) / (1 * 2 * 3) = 10 Zustände:

Wir suchen darin einen längsten Weg. (Übungsaufgabe: Einen Hamiltonkreis gibt es sicher nicht. Beweise das ohne Zuhilfenahme des Folgenden.)
Wir sehen, daß in diesem Graphen die Kanten, die mit 0 oder h beschriftet sind, disjunkte Schleifen erzeugen Man kann leicht zeigen, daß in einem Prim-Muster aus jedem Kreis wenigstens ein Zustand fehlen muß.
Wir fragen nun nach den (b,h), für die diese Schranke erreicht werden kann.
Einige Daten (ausgerechnet von Jack Boyce) sind hier. Erklärung zur Notation:
3 Balls
6: ++2-+-+2-++-5--
++2-+-+11++-5--
++1+--+4-+-+4--
++1+--+4-+-+13-
++1+--55-+-+4--
+35-+-+2-++-5--
N(skips) = {2,0,4,0} ( 15/ 16/ 20)
die 6 ist die maximale Wurfhöhe. Ein + bedeutet eine 6,
ein - bedeutet eine 0.
Die 20 sagt, daß es insgesamt 6 über 3 = (6 * 5 * 4) / (1 * 2 * 3) = 20 verschiedene Zustände gibt. Diese zerfallen in 3 Kreise der Länge 6:
xxx---, xx---x, x---xx, ---xxx, --xxx-, -xxx-- xx-x--, x-x--x, -x--xx, x--xx-, --xx-x, -xx-x- xx--x-, x--x-x, --x-xx, -x-xx-, x-xx--, -xx--xsowie einen Kreis der Länge 2
x-x-x-, -x-x-xDas sind Konjugationsklassen, siehe Kapitel 1, Abschnitt 1.3 in Lothaire: Combinatorics on Words (1983).
Nach dem oben nicht bewiesenen Satz muß aus jedem Kreis wenigstens ein Zustand fehlen. Das heißt, der längste Weg hat höchstens 20 - 4 = 16 Zustände. Das ist die Zahl in der Mitte von (15/ 16/ 20).
Die 15 ist die Länge der tatsächlich gefundenen längsten Wege. Das ist also in diesem Fall eins kürzer als erwartet. Genau solche Unterschiede gilt es zu begründen.
Siehe auch rec.juggling-posts von Jack Boyce und Steven de Rooij