Nächste Seite: Semantik von Programmiersprachen Aufwärts: Prinzipien von Programmiersprachen Vorlesung Vorherige Seite: Einleitung
Token-Typen sind üblicherweise
=, +, &&, ...)
Beispiele:
man kann eine formale Sprache beschreiben durch:
Bsp: reguläre Ausdrücke
![$ \begin{array}{ll}
& (p<r \wedge w[p]=a \wedge w[r]=c) \\
\Rightarrow & \exists q: (p<q \wedge q<r\wedge w[q]=b)
\end{array}$](img3.png)
Aus Sprachen L1, L2
Def: Sprache regulär :
Satz: Durchschnitt und Differenz braucht man dabei nicht.
Die Menge E(Σ)
(autotool: Ziffern oder Kleinbuchstaben)
Wir fixieren das Alphabet
Σ = {a, b}
die trotzdem nur reguläre Sprachen erzeugen
Beispiel:
Σ*
Beispiel: exakte Wiederholungen
L
beachte Unterschied zu Lk
auch reguläre Operatoren werden gern schlecht
implementiert
(http://swtch.com/~rsc/regexp/regexp1.html)
Wie beweist man
w∈L(X)
(Wort w
beweise
w∈L(X1)
zerlege
w = w1⋅w2
wähle einen Exponenten
k∈
w = abb⋅a = ab2⋅ab0∈ab*⋅ab*⊆(ab*)2⊆(ab*)*
Beispiel für Distributivgesetz?
Welches sind jeweils die neutralen Elemente der Operationen?
(vgl. oben) Welche Relation auf Sprachen (Mengen)
ergibt sich als „Teilbarkeit`` bzgl. ∪
Welche Notation wird für unsere Operatoren +
Berechnungs-Modell (Markov-Algorithmen)
Regelmenge
R⊆Σ*×Σ*
Regel-Anwendung:
u→Rv
Beispiel: Bubble-Sort:
{ba→ab, ca→ac, cb→bc}
Beispiel: Potenzieren:
ab→bba
Aufgaben: gibt es unendlich lange Rechnungen für:
R1 = {1000→0001110}, R2 = {aabb→bbbaaa}
(üblich: Kleinbuchst., Ziffern)
(üblich: Großbuchstaben)
R⊆(Σ∪V)*×(Σ∪V)*
Tokenklassen sind meist reguläre Sprachen.
Programmiersprachen werden kontextfrei beschrieben
(mit Zusatzbedingungen).
(=
jede Regel hat die Form
(vgl. lineares Gleichungssystem)
Beispiele
Für jede Sprache L
Beweispläne:
LA(p, q, r) =
Def (Wdhlg): G
geeignet zur Beschreibung von Sprachen mit
hierarchischer Struktur.
Bsp: korrekt geklammerte Ausdrücke:
G = ({a, b},{S}, S,{S→aSbS, S→ε})
Bsp: Palindrome:
G = ({a, b},{S}, S,{S→aSa, S→bSb, S→ε)
Bsp: alle Wörter w
Abstraktion von
vollständig geklammerten Ausdrücke
mit zweistelligen Operatoren
Höhendifferenz:
h : {a, b}*→
Präfix-Relation:
u≤w :
Dyck-Sprache:
D = {w | h(w) = 0∧∀u≤w : h(u)≥0}
CF-Grammatik:
G = ({a, b},{S}, S,{S→ε, S→aSbS})
Satz: L(G) = D
L(G)⊆D
D⊆L(G)
(Induktionsbehauptung? Induktionsschritt?)
Backus-Naur-Form (BNF)
Erweiterte BNF
Cox 2007
http://swtch.com/~rsc/regexp/regexp1.html
Def: ein geordneter Baum T
Def: der Rand eines geordneten, markierten Baumes (T, m)
Beachte: die Blatt-Markierungen sind
∈{ε}∪Σ
Für Blätter:
rand(b) = m(b)
Satz:
w∈L(G)
Def: G
Bsp: ist
{S→aSb| SS| ε}
(beachte: mehrere Ableitungen
S→R*w
Die naheliegende Grammatik für arith. Ausdr.
Auswege:
Grammatik-Regeln
Grammatik-Regel
Ziele:
Übung:
naheliegende EBNF-Regel für Verzweigungen:
Dieser Satz hat zwei Ableitungsbäume:
![]() L2
L2
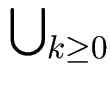 L1k
L1k
![]()
über einem Alphabet (Buchstabenmenge) Σ
ist die kleinste Menge E
Jeder solche Ausdruck beschreibt eine reguläre Sprache.
Eps)
Empty)
* oder weglassen)
+)
^*)
wenn nicht-reguläre Sprachen entstehen können,
ist keine effiziente Verarbeitung (mit endlichen
Automaten) möglich.
![]() (Σ*abΣ*)2
(Σ*abΣ*)2
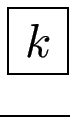 : = {wk | w∈L}
: = {wk | w∈L}
Beispiel:
w = abba, X = (ab*)*
![]()
![]() ∃x, z∈Σ*,(l, r)∈R : u = x⋅l⋅z∧x⋅r⋅z = v
∃x, z∈Σ*,(l, r)∈R : u = x⋅l⋅z∧x⋅r⋅z = v
Grammatik G
(Wort-Ersetzungs-System)
Grammatik
{ terminale
= mkSet "abc"
, variablen
= mkSet "SA"
, start = 'S'
, regeln = mkSet
[ ("S", "abc")
, ("ab", "aabbA")
, ("Ab", "bA")
, ("Ac", "cc")
]
}
von G
Anweisung -> Bezeichner = Ausdruck
| if Ausdruck then Anweisung else Anweisung
Ausdruck -> Bezeichner | Literal
| Ausdruck Operator Ausdruck
(4*(5+6)-(7+8))
⇒
(()())
⇒aababb
![]() : w
: w ![]() | w|a - | w|b
| w|a - | w|b
![]() ∃v : u⋅v = w
∃v : u⋅v = w
![]()
<assignment> -> <variable> = <expression>
<number> -> <digit> <number> | <digit>
kann in BNF übersetzt werden
<digit>^+
if <expr> then <stmt> [ else <stmt> ]
merke:
![]()
expr -> number | expr + expr | expr * expr
ist mehrdeutig (aus zwei Gründen!)
![]()
was
x ![]() y
y ![]() z
z
(3 + 2) + 4
 3 + 2 + 4
3 + 2 + 4 3 + (2 + 4)
3 + (2 + 4)
(3 - 2) - 4
 3 - 2 - 4
3 - 2 - 4 3 - (2 - 4)
3 - (2 - 4)
(3**2)**4
 3**2**4
3**2**4 3**(2**4)
3**(2**4)
X1 + X2 + X3 auffassen als (X1 + X2) + X3
Ausdruck -> Zahl | Ausdruck + Ausdruck
ersetzen durch
Ausdruck -> Summe
Summe -> Summand | Summe + Summand
Summand -> Zahl
 3 + 2*4
3 + 2*4 3 + (2*4)
3 + (2*4)
summand -> zahl
erweitern zu
summand -> zahl | produkt
produkt -> ...
(Assoziativität beachten)
Festlegung:
Realisierung in CFG:
bei Kombination eines Operators mit sich
bei Kombination verschiedener Operatoren
<statement> -> if <expression>
then <statement> [ else <statement> ]
führt zu einer mehrdeutigen Grammatik.
if X1 then if X2 then S1 else S2
else
gehört immer zum letzten verfügbaren then.
<statement>, <statement-no-short-if>