Nächste Seite: Logarithmen Aufwärts: Zahlen Vorherige Seite: Themen
Wie bestimmt man schnell viele Ziffern von  ?
?
Idee: Potenzreihe (Satz von Taylor)
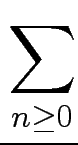
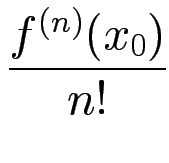 dn
dn
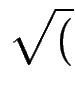 1 + d )= 1 + d /2 - d2/8 + 5d3/24 +5d4/27 - ...
1 + d )= 1 + d /2 - d2/8 + 5d3/24 +5d4/27 - ...
konvergiert aber zu langsam für d = 1
Trick:
52*2 ![]() 72, also
72, also
 = 7/5 .
= 7/5 . 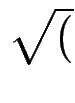 1 + 1/49)
1 + 1/49)
(Aufgabe: für 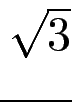 )
)
(wo kommen diese Brüche her? Kettenbrüche!)