Nächste Seite: Gröbnerbasen Aufwärts: Polynome Vorherige Seite: Polynome in mehreren Variablen
arithmetisches Mittel
A(x1,..., xn) = ( xi)/n,
geometrisches Mittel
G(x1,..., xn) =
xi)/n,
geometrisches Mittel
G(x1,..., xn) = ![$\sqrt[n]{{\prod x_i)}}$](img83.png) .
.
Aufgabe: Stelle A(x1,…, x4)4 - G(x1,…, x4)4 als Summe von Quadraten (SOS) von Polynomen dar.
Hinweis: A(x1, x2)2 - G(x1, x2)2 = (x1 - x2)2/4 und
A(x1, x2, x3, x4) = A(A(x1, x2), A(x3, x4))≥A(G(x1, x2), G(x3, x4))≥G(G(x1, x2), G(x3, x4)) = G(x1, x2, x3, x4).
Zusatz: A(x1, x2, x3)3 - G(x1, x2, x3)3 ist kein SOS, kann aber als Bruch mit SOS im Zähler und (x + y + z) im Nenner geschrieben werden. Dazu die SOS-Darstellung der A-G-Ungleichung für die 4 Werte x1, x2, x3, t = A(x1, x2, x3) benutzen, denn A(x1, x2, x3, t) = t und G(x1, x2, x3, t)4 = G(x1, x2, x3)3⋅t.
Hintergrund: Bruce Reznick: Some Concrete Aspects of Hilbert's 17th Problem, 2000, https://faculty.math.illinois.edu/~reznick/.
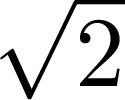 +
+ ![$\sqrt[3]{{3}}$](img5.png) nach angegebenem Verfahren ausrechnen und überprüfen.
nach angegebenem Verfahren ausrechnen und überprüfen.
Ähnlich für
 +
+ 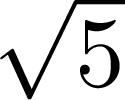 oder (z.B.)
oder (z.B.)
![$\sqrt[5]{{3}}$](img85.png) +
+ ![$\sqrt[5]{{5}}$](img86.png)
o.B.d.A A1 = A2 = B1 = 0 annehmen.
Warum wäre zusätzlich C2 = 0 doch eine B.d.A.?
eine anderen Koeffizientenbereich (als Rational)
benutzen, z.B. Complex Rational
nichttriviale Rechnungen durchführen (z.B. Division von Xpq - 1 durch Xp - 1), Ergebnis prüfen,
Laufzeit messen, Ausführung profilieren, teure Funktionen feststellen, ggf. verbessern
Vergleichen mit derselben Rechnung in einem richtigen Computer-Algebra-System (maxima, fricas). (Nicht irgendwo online, sondern lokal, damit man messen und vergleichen kann.)