Nächste Seite: Programme Aufwärts: Daten Vorherige Seite: Konstruktor-Systeme
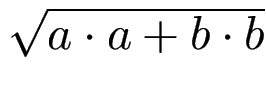 an.
an.
mit ghci:
data T = F T | G T T T | C deriving Show
erzeugen Sie o.g. Terme (durch Konstruktoraufrufe)
Die Größe eines Terms t ist definiert durch
| f (t1,…, tk)| = 1 + 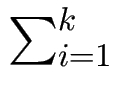 | ti|.
| ti|.
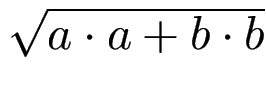 |.
|.
Vervollständigen Sie die Definition der Tiefe von Termen:
| depth(f ()) = 0 | |||
| k > 0 | ⇒ | depth(f (t1,…, tk)) = ... |
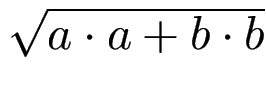 )
)
Für die Signatur Σ = {Z/0, S/1, f /2}:
Notation für Termersetzungsregeln: anstatt (l, r) schreibe l→r.
Abkürzung für Anwendung von 0-stelligen Symbolen: anstatt Z() schreibe Z.
bestimme alle R-Normalformen von f (S(Z), S(Z)).
bestimme alle Rd-Normalformen von d (d (S(Z))).
Bestimme die Menge der Terme aus Term(Σd), die Rd-Normalformen sind.
definiere Terme t0 = D, ti+1 = A(ti, D).
Zeichne t3. Bestimme | ti| .
bestimme S-Normalform(en), soweit existieren, der Terme t2, t3, t4. Zusatz: von ti allgemein.
Abkürzung für mehrfache Anwendung eines einstelligen Symbols: A(A(A(A(x)))) = A4(x)
über Signatur {A/1, B/1, E/0}:
bestimme Normalform von Ak(Bk(E))
für k = 1, 2, 3, allgemein.
über Signatur {A/1, B/1, E/0}:
bestimme Normalform von Ak(B(E))
für k = 1, 2, 3, allgemein.
Johannes Waldmann 2014-07-10