Entscheidungsverfahren (Ansatz)

Def.: Menge M⊂$\mathbb {N}$^k heißt P-definierbar

$\iff$ es gibt eine P-Formel F so daß M = Mod(F)

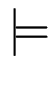wobei Mod(F) : = {m∈$\mathbb {N}$^k | {x₁ $\mapsto$ m₁,…, x_k $\mapsto$ m_k} $\models$ F}

für F mit freien Var. x₁,…, x_k,

Satz: jede solche Modellmenge Mod(F) ist effektiv regulär:

• es gibt einen Algorithmus, der zu jeder P-Formel F ...
• ...einen endl. Automaten A konstruiert mit Lang(A) = Kodierung vonMod(F)

Folgerung: Allgemeingültigkeit ist entscheidbar:

Lang(A) = ∅ gdw. Mod(F) = ∅ gdw. F ist widersprüchlich gdw. ¬F ist allgemeingültig.