Bitonisches Zählen und Zusammenfügen (II)

Induktionsschritt:

M_2n($\vec{{x}}$,$\vec{{y}}$) = $\left\{\vphantom{ \begin{array}{l} M_n(\operatorname{odd}\vec{x},\operatorname... ...rname{odd}\vec{y}); \\ V(x_1,x_2);\ldots; V(y_{n-1},y_n) \end{array}}\right.$$\begin{array}{l} M_n(\operatorname{odd}\vec{x},\operatorname{even}\vec{y}) ;\\... ...\operatorname{odd}\vec{y}); \\ V(x_1,x_2);\ldots; V(y_{n-1},y_n) \end{array}$

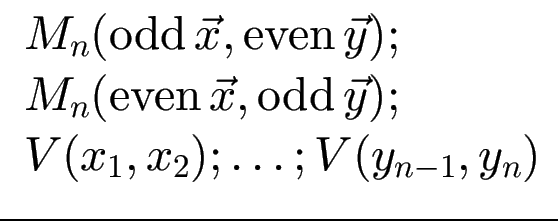
mit V(p, q) = Verteiler, odd(x₁, x₂,…) = (x₁, x₃,…), even(x₁, x₂,…) = (x₂, x₄,…).

Satz: jedes solche M_n erfüllt die Spezifikation.

Übung: konstruiere C₄, M₄

Übung: Beweis für M₈ mit Eingangsfolge (3, 3, 2, 2;4, 3, 3, 3), unter der Annahme, daß der Satz für M₄ gilt.

Übung: Beweis für M_2n mit beliebiger Eingangsfolge,
unter der Annahme, daß der Satz für M_n gilt.