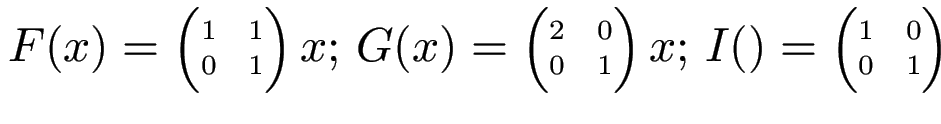In jeder Algebra gelten diese Formeln:
(t1 = s1)∧…∧(tk = sk)→f (t1,…, tk) = f (s1,…, sk)
mathend000#
(Leibniz-Axiom für die Gleichheit, functional consistency)
- Definition: eine Σ
mathend000#-Algebra heißt frei,
wenn keine Gleichheiten gelten, die nicht aus o.g. Axiomen folgen.
- Beispiel: jede Termalgebra ist frei.
- Nicht-Beispiel:
Σ = { + , 1}, D =
 mathend000# ist nicht frei.
mathend000# ist nicht frei.
- Ü: eine freie Algebra auf
 mathend000# zur Signatur {f /2}
mathend000#?
mathend000# zur Signatur {f /2}
mathend000#?
- Ü: die von
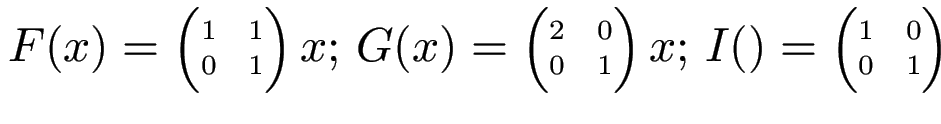 mathend000#
erzeugte Algebra ist frei?
mathend000#
erzeugte Algebra ist frei?
2014-03-31