Nächste Seite: Lösungsansätze Aufwärts: SMT (satisfiability modulo theory) Vorherige Seite: Anwendungsaufgabe
Wortersetzungssystem R über ![]() ,
,
Bsp:
R = {aa![]() aba} über
aba} über
![]() = {a, b}
= {a, b}
Matrix-Interpretation (Halbring D, Dimension n)
[ . ] : ![]()
![]() Dn×n
für Buchstaben
Dn×n
für Buchstaben
für Wörter durch Multiplikation: [x1,..., xk] = [x1]o...o[xk]
zulässig:
![]() x
x ![]()
![]() : [x]1, 1
: [x]1, 1 ![]() 0D
0D
kompatibel:
![]() (l, r)
(l, r) ![]() R :
R : ![]() i, j : [l]i, j > 0[r]i, j
i, j : [l]i, j > 0[r]i, j
wobei
p > 0q![]() (p = 0D = q)
(p = 0D = q) ![]() (p > q)
(p > q)
Beispiel:
D = (![]()
![]() { +
{ + ![]() }, min, max),
}, min, max),
[a] = 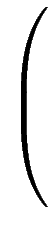
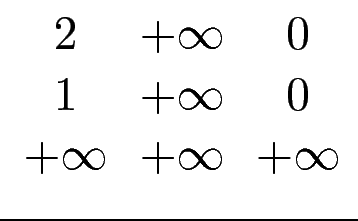
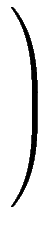 ,[b] =
,[b] = 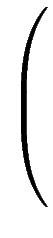
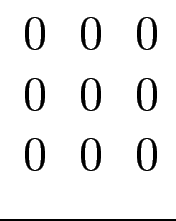
 .
.