Nächste Seite: Erweiterungen Aufwärts: SMT (satisfiability modulo theory) Vorherige Seite: (Un)Gl. zwischen Polynomen
(Wiederholung F-M)
![]() x : K1
x : K1![]() x
x ![]() ...
...![]() Kp
Kp![]() x
x ![]() x
x![]() G1
G1 ![]() ...
...![]() x
x![]() Gq
Gq
![]()
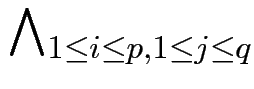 Ki
Ki![]() Gj
Gj
vergleiche mit Resolution:
| (A |
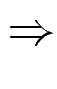 |
(A |
|
(¬A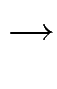 x) x) 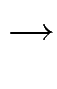 B) B) |
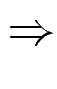 |
(¬A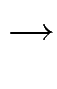 B) B) |
|
| (¬A |
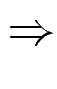 |
(¬A |
Elimination von x durch vollständige Resolution
(A1 ![]() x,..., Ap
x,..., Ap ![]() x)
mit
(¬x
x)
mit
(¬x ![]() B1,...,¬x
B1,...,¬x ![]() Bq)
Bq)
Übung: unit propagation als Spezialfall
Projekt: SAT-Solver bzw. Präprozessor bauen