Quantifizierte Boolesche Formeln

Syntax: eine QBF hat die Form $\underbrace{{Q_1 v_1 \ldots Q_n v_n }}_{{\text{Pr\uml {a}fix}}}^{}$$\underbrace{{M}}_{{\text{Matrix}}}^{}$,

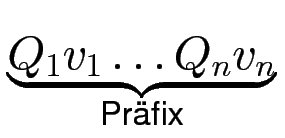
wobei Q₁,..., Q_n $\in$ {$\forall$,$\exists$} und M eine aussagenlogische Formel ist (die die Variablen v₁,..., v_n enthalten kann)

Semantik: val(M) = val(M,$\emptyset$) mit

val($\forall$xM, b) = val(M, b $\cup$ {(x, 0)}) $\wedge$ val(M, b $\cup$ {(x, 1)})

val($\exists$xM, b) = val(M, b $\cup$ {(x, 0)}) $\vee$ val(M, b $\cup$ {(x, 1)})