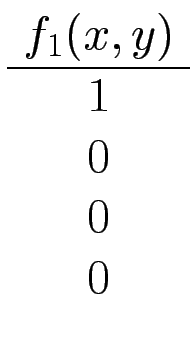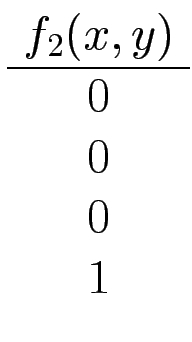Basis-Satz (Beweis-Idee)

Man stellt f als Disjunktion von Funktionen f₁, f₂,... dar (je eine Funktion für jede 1 in der Wertetabelle von f)

x y f (x, y)

0 0 1

0 1 0

1 0 0

1 1 1

    $$\begin{array}{cc\vert c} f_1(x,y) \hline 1 \\ 0 \\ 0 \\ 0 \end{array}$$    $$\begin{array}{cc\vert c} f_2(x,y) \hline 0 \\ 0 \\ 0 \\ 1 \end{array}$$

Jedes solche f_i hat dann genau eine 1 in seiner Wertetabelle, kann also selbst als Konjunktion dargestellt werden.

f₁(x, y) = ¬x $$\wedge$$ ¬y,    f₂(x, y) = x $$\wedge$$ y