Wertetabellen

Für jedes f : $\mathbb {B}$^k$\to$$\mathbb {B}$ ist der Definitionsbereich endlich. (Wie groß genau?)

Die Funktion f kann deswegen durch eine Wertetabelle gegeben werden. Beispiele:

x y f (x, y)

0 0 0

0 1 1

1 0 1

1 1 1

        $$\begin{array}{cc\vert c} x & y & g(x,y) \hline 0 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \end{array}$$    $$\begin{array}{cc\vert c} x & y & h(x,y) \hline 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \end{array}$$

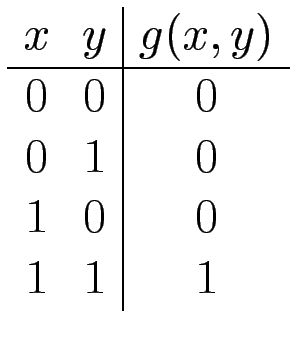
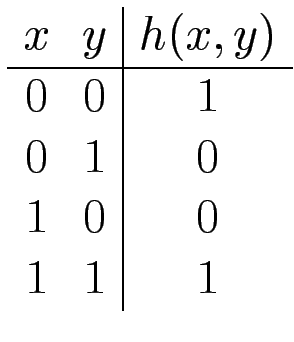
Für jedes k gibt es nur endlich viele verschiedene k-stellige Boolesche Funktionen. (Wieviele genau?)