LCS

Idee: die beiden Aufgaben sind äquivalent:

• kürzeste Edit-Sequenz finden
• längste gemeinsame Teilfolge (longest common subsequence) finden

Beispiel: y = AB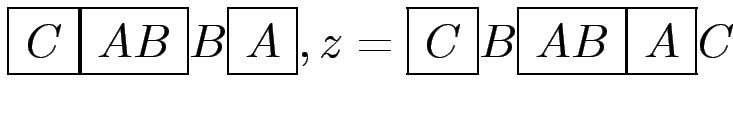$\fbox{\ensuremath{C}}\fbox{\ensuremath{AB}}B\fbox{\ensuremath{A}}, z = \fbox{\ensuremath{C}}B\fbox{\ensuremath{AB}}\fbox{\ensuremath{A}}C$

für x = CABA gilt x$\le$y und x$\le$z,

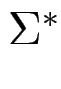wobei die Relation $\le$ auf $\Sigma^{*}_{}$ so definiert ist:

u$\le$v, falls man u aus v durch Löschen einiger Buchstaben erhält (jedoch ohne die Reihenfolge der übrigen Buchstaben zu ändern)

vgl. mit Ausgabe von diff